投下したπなぞぷよの解き方講座(自己流)

因みにかなりがっつり

需要があるかないかわからないのでかなり雑で見にくいかもかも

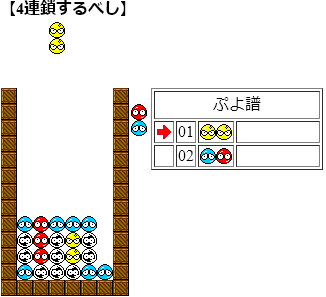
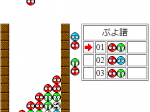
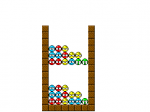
1問目

解答

解説：ぷよの各色の個数から飽和連鎖問題である。青の連結を考えると、2列目に必ず青が必要。発火色は赤or青なので、2手目は2縦に限られる。試しに消してみると赤を消した後、青は繋がらない。即ち、次に消えるのは黄であり、それを実現するためには黄ゾロは3縦しかありえない。

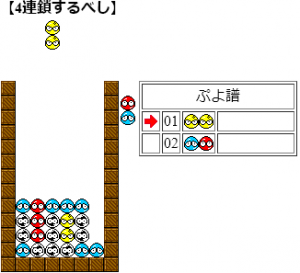
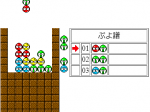
2問目

解答

解説：ぷよ数より飽和連鎖問題。故に発火場所は左の青、上の赤、右の赤である(ツモが青２赤２なのでツモで発火点は作れない)。ここで右上の青はこの2手では届かないことに注意する。上の赤は左と上から発火可能性があるが、左は2列目4段目にぷよがある必要があり、青の3連結を消さないこととツモより、そこには赤しか置けない。しかし、そうした場合上赤左発火が5連結となり、飽和連鎖に反する。また、上赤上発火だと仮定すると、赤の次に青しか消す候補がない。固ぷよの存在により青の降ってくる位置は4列目しかありえず、赤発火なので2手目は4縦である。ここで「発火位置に発火手以外のぷよを置けない法則」から1手目を4列目に置くことはできない。従って1手目は下の赤に繋げるため5縦になるが、このとき青が分離されるので、これは矛盾。

次に右下赤発火だと仮定すると、連鎖の流れは赤→青→黄となる。このとき2手目は56横か6縦となる。これ即ち青ぷよが56列目にしかないことを意味し、1手目の青を4列目以降に置く必要がある。このことから1手目の赤ぷよの置ける位置も3列目以降に限られる。しかし4列目には赤の3連結が露出しているため不適。さらに5列目は2手目で発火した際に巻き込まれるため不適。6列目は消えてしまうため自明に不適。故に1手目は34横に限られれる。しかしこれでは赤が消えないため、結論として右下赤発火は不適。

従って左の青発火に限られる。このとき連鎖の流れは青→黄→赤となる。ここで2列目に赤を乗せた場合３連鎖目の赤が5連結以上になるため不適。故に2手目は23横置きに限られる(1縦は2列目に赤を必要とするため不適)。ここで4連鎖目に消えるぷよは赤と青いずれも考えられる。赤が消えるときを考えるが、この時2手目が23横なので3列目のどこかに赤が置かれることに注意する。このとき連鎖の段階で5列目が4列目より下がることがないため3列目に赤を二つ置く必要があるが、この場合2連鎖目に赤が同時消しになってしまうため不適。従って4連鎖目は青である。青が4連鎖目に消えるためには3列目か6列目に青がある必要があり、1手目はそれぞれ3縦か56横である。それぞれ検証すれば56横が求めるべき答えとわかる。

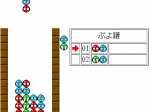
3問目

解答

解説：簡単のため、左上青＝①、右上赤＝②、左下赤＝③、右下青＝④とおく。ぷよ数から飽和連鎖問題である。よって黄色の位置から1，2手目で2，3列目に黄ぷよを1つずつ置かねばならない。よって1，2手目で1，6列目にぷよを置くことができない。また発火位置は①～④全て考えられるが、このうち③④発火は２連鎖目が６連結になってしまうため不適。従って①②いずれかが発火位置である。

ここでまず5連鎖となる完成形を考える。ここで対称性から①発火としてもよい。このとき連鎖の流れは①→②→④→③→黄、①→③→④→②→黄、①→③→②→④→黄の3通りが考えられる。ここで①→③のルートは3列目10段目に暴発回避のため黄色しか置けないことから、2列目赤青縦発火に限られる。ここで①が消えた後暴発しないために3列目は下から順に黄青の順に置く必要がある。この時3連鎖目が④になるので、①→③→②→④→黄のルートは不適。同時に3列目に黄青に続き赤を乗せると③が消えるときに②が同時に消えてしまう。従って、①→③→④→②→黄も不適。よって5連鎖のルートは①→②→④→③→黄に限られる。先ほどの考えで3列目10段目には黄色が乗る。②繋げるためその上に赤、また2列目が発火位置であるとこまで決まる。次に消える④の青の受けは4，5列目である。4列目に青が乗るとき、その上に赤黄の順でも黄赤の順でも5連鎖を実現できる。5列目に青が乗るとき、4列目に下から黄赤の順で乗せることで実現できる。従って5連鎖を実現できるのは以上の3通りと対称性から反転して赤と青を入れ替えた、計6通りである。流石にわかりにくいので一覧にした。

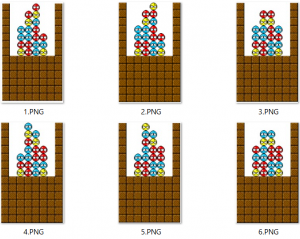
ここで見ればわかる通り、4,5は発火手以外で3列目が12段目まで置かれているので、これはなぞぷよ基本ルールの不可能設置の公理より不適。

次にそれを実現するツモ捌きを考える。まず発火手の赤青について考える。1～3はいずれも23横置きしかない。よって4列目の赤は1手目で置く必要がある。しかし、1,2は青が挟まっているので実現不可能。よって可能性があるのは3だが、そのとき1手目は4縦しかなく、右の青ぷよ1個が孤立してしまう。ツモは組ぷよしかないのでこれを実現できない。よって残るのは6であり、これは1手目：23横、2手目：34横、3手目：45横とすることで実現でき、これが求めるべき答えである。

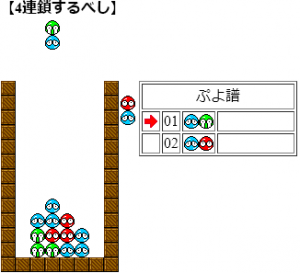
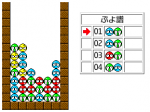
4問目

解答

解説：ちょっとがっつり解説が大変になってきたのと、これは閃きなぞぷよなのでポイントを紹介する。

ぷよ数より飽和連鎖問題である。今回ツモに緑が4つある。故に発火点を作り出せる問題であることに注意する。

5連鎖のルートとしてぱっと見みえるのは、中緑→赤→黄→青→下緑、中緑→赤→黄→下緑→青、下緑→赤→青→黄→中緑が考えられるが、実現できない。露骨に1列目があいており、2列目の色に緑がないことから、ツモの緑を1列目に4連結発火が考えられ、この発火の仕方はツモの順から1通りで、それが答えである。

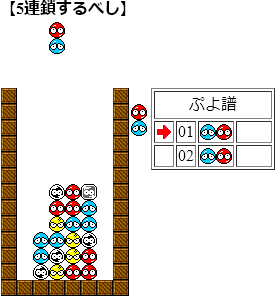
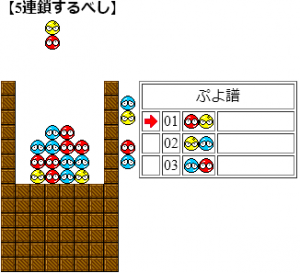
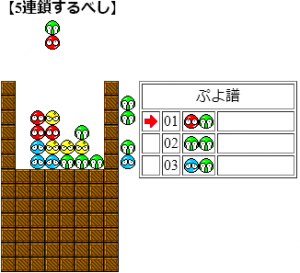
5問目

解答

解説：青の露出と緑の位置から初手の置き方は12横、2縦、3縦、4縦の4通りである。12横のとき2列目の青は1列目の青と消えなければならない。しかし、そのためには緑を消す必要があり、だが緑を消すために2列目の青を消す必要があり、矛盾である。次に2縦のとき、緑を消すためには上の青を消さなければならないがこれは2手目でしかできない。すると、2列目の孤立青と下の青が完全分離され、不適。次に初手4縦を考えると、緑が消えるために右下の赤青を消す必要がある。初手の青で右下の青を消せないので、2手目で右下の赤青を消すには4縦(2通り)しかない。しかし、いずれでも左上青が同時消しとなり矛盾。従って残る初手は3縦である。

3縦のとき、緑を消すために左上青と赤を消さねばならない。1手目の青は緑の上にあるので不可。故に2手目で赤青を消すには4列目に下から青赤の順で置くしかなく、これが求めるべき答えである。

以上が解答解説である。なぞぷよの解き方は大きく4種類あります。

１：2問目パターン：ツモの制約からおける場所をどんどん絞っていくタイプ

２：3問目パターン：完成形を先に作り、あとからツモを当てはめていくタイプ

３：4問目パターン：なぞぷよでよくあるタイプの発火や連鎖などで、閃き、特に経験量がものをいうタイプ

４：虱潰しパターン：全消し問題などは、手数が増えると理詰めでは到底絞り込めないので、片っ端から試し、経験と直感で正解ルートを模索するタイプ

処理としては3→1→2→4の順で考える。

今回の解説は最も時間のかかる場合である。通常は検証途中に正解がみつかる。また、上級なぞぷよらーになるほど、3の経験量の領域と処理速度が大幅に上昇する。

大体こんな感じである。そもそもこんなにちゃんと書いても、ここまでガチでやる人は果たしているのだろうか。
可能性の絞り方と、矛盾の出し方を細かく書いたので、今までむやみやたらにやっていた人にとっては、少しは役に立つかも？

何か指摘や、解説不足なとこありましたら報告してください。

ではでは～